Jan 15, · The integral of a function f(x) with respect to x is written as \(\int f(x)\;dx\) Also, integration is considered as almost an inverse to the operation of differentiation means that if, \({d\over dx}f(x)=g(x)\) then \(\int g(x)\;dx=f(x)C\) The extra C called the constant of integration, which is really necessaryWe can take the antiderivative of both sides to give f(x)g(x) = Z f(x)g0(x)dx Z g(x)f0(x)dx;In this tutorial you are shown how to do integrals of the form f '(x) / f (x) Why the Modulus Sign?

Indefinite Integrals Sums Multiples Video Khan Academy
How to integrate f(x)
How to integrate f(x)-8 Suppose we get the following general case ∫ 0 1 f ( x) f ′ ( 1 − x) d x where f is differentiable on 0, 1 Can we have a general formula for the integral ?So the area is \(A = ∫ab f(x)g(x) dx\) and put those values in the given formula Then solve the definite integration and change the values to get the result You can calculate the area and definite integral instantly by putting the expressions in the area between two curves calculator




Ex 7 9 Direct Integrate X Ex Sin Pi X 4 Dx Ex 7 9
F (x) g0(x) dx = f (x) g(x) − Z f 0(x) g(x) dx We need to choose the functions f and g They should be chosen in a way that the righthand side above is simpler to integrate than the original lefthand side f (x) = x, g0(x) = e2x ⇒ f 0(x) = 1, g(x) = e2x 2 Z x e2x dx = x e2x 2 − Z e2x 2 dx = x e2x 2 − e2x 4 c We conclude I = e2x 4 (2x − 1) c CIntegral Calculus Formula Sheet Derivative Rules 0 d c dx nn 1 d xnx dx sin cos d x x dx sec sec tan d x xx dx tan sec2 d x x dx cos sin d x x dx csc csc cot d x xx dx cot csc2 d x x dx d aaaxxln dx d eex x dx dd cf x c f x dx dx ddd f x gx f x gx dx dx dx fg f g f g 2 f fg fg gg d fgx f gx g x dxDifferentiation Formulas List In all the formulas below, f' means \( \frac{d(f(x))}{dx} = f'(x)\) and g' means \(\frac{d(g(x))}{dx}\) = \(g'(x)\) Both f and g are the functions of x and differentiated with respect to x We can also represent dy/dx = D x y Some of the general differentiation formulas are;
Sep 12, · Formulas for the comparison theorem The comparison theorem for improper integrals is very similar to the comparison test for convergence that you'll study as part of Sequences & Series It allows you to draw a conclusion about the convergence or divergence of an improper integral, without actually evaluating the integral itself Hi!Second, the boundaries of the region are called the limits of integration We call the function f (x) f (x) the integrand, and the dx indicates that f (x) f (x) is a function with respect to x, called the variable of integration In the following exercises, evaluate the integral using area formulasThe result—called the Laplace transform of f—will be a function of p, so in general, Example 1 Find the Laplace transform of the function f( x) = x By definition, Integrating by parts yields Therefore, the function F( p) = 1/ p 2 is the Laplace transform of the function f( x) = x Technical note The convergence of the improper integral here depends on p being positive, since only
Integral formulas Definite integral of a complexvalued function of a real variable Consider a complex valued function f(t) of a real variable t f(t) = u(t) iv(t), which is assumed to be a piecewise continuous function defined in the closed interval a ≤ t ≤ b The integral of f(t) from t = a to t = b, is defined as Zb a f(t) dt = Zb a u(t) dt i Zb aThe definite integral f(x) is a function that obtains the answer of the question " What function when differentiated gives f(x) An indefinite integral has no lower limit and the upper limit on the integrals and obtains the answer that has variable x in it and alsoIn calculus, the chain rule is a formula to compute the derivative of a composite function That is, if f and g are differentiable functions, then the chain rule expresses the derivative of their composite f ∘ g — the function which maps x to f {\displaystyle f} — in terms of the derivatives of f and g and the product of functions as follows ′ = ⋅ g ′ {\displaystyle '=\cdot g'} Alternatively, by letting h = f ∘ g




All Integration Formulas Complete List Of Integrals Cuemath




4 1 4 2 Integration Techniques Trigonometric Functions Sine
U(x) = Z G(x;x 0)f(x 0)dx 0 (2) If such a representation exists, the kernel of this integral operator G(x;x 0) is called the Green's function It is useful to give a physical interpretation of (2) We think of u(x) as the response at x to the influence given by a source function f(x) For example, if the problem involved elasticity, umightZ f(x)g0(x)dx = f(x)g(x) Z g(x)f0(x)dx In Leibnitz notation, taking u = f(x), du = f0(x)dx and v = g(x), dv = g0(x)dx ZJan 02, 21 · Arc Length = ∫b a√1 f′ (x)2dx Note that we are integrating an expression involving f′ (x), so we need to be sure f′ (x) is integrable This is why we require f(x) to be smooth The following example shows how to apply the theorem Example 641 Calculating the Arc Length of a Function of x Let f(x) = 2x3 / 2




Ppt 12 5 The Fundamental Theorem Of Calculus Powerpoint Presentation Id




Bsnl Tta Match Point Applied Mathematics Integration And Differentiation I All Exam Review
Dec , · Figure 613 The area bounded by the functions f(x) = (x − 1)2 1 and g(x) = x 2 on the interval 0,3 The area between the two curves on 0, 3 is thus approximated by the Riemann sum and then as we let n → ∞, it follows that the area is given by the single definite integral A = ∫3 0(g(x) − f(x))dxJan 29, 13 · It's always simpler to integrate expanded polynomials, so the first step is to expand your squared binomial (x 1/x)² = x² 2 1/x² Now you can integrate each term individually ∫ (x² 2 1/x²)dx = ∫x²dx ∫2dx ∫ (1/x²)dx Each of those terms are simple polynomials, so they can be integrated with the formulaUsing Integration by Parts Use integration by parts with u = x and dv = sinxdx to evaluate ∫xsinxdx Solution By choosing u = x, we have du = 1dx Since dv = sinxdx, we get v = ∫sinxdx = −cosx It is handy to keep track of these values as follows u = x




Practical Integration By Parts Calculus




The Definite Integral And Ftc
318 Chapter 4 Fourier Series and Integrals Zero comes quickly if we integrate cosmxdx = sinmx m π 0 =0−0 So we use this Product of sines sinnx sinkx= 1 2 cos(n−k)x− 1 2 cos(nk)x (4) Integrating cosmx with m = n−k and m = nk proves orthogonality of the sinesA f x g x dx= −∫ d ( ) ( ) c A f y g y dy= −∫ cb ( ) ( ) ( ) ( ) ac A f x g x dx g x f x dx= − −∫∫ Volumes of Revolution The two main formulas are V A x dx=∫ ( ) and V A y dy=∫ ( ) Here is some general information about each method of computing and some examples Rings Cylinders (( )22 ( ) ) A =π outer radius inner radius− A =2πò f '(x)g(x)dx = f(x)g(x) ò f(x)g'(x)dx This is the "integration by parts" formula Whenever you have an integral where the integrand is the product of two functions, you can try to use this formula It is most useful when integrating or differentiating one of the functions in the product will simplify that function For example, when you




7 Techniques Of Integration Copyright C Cengage Learning All Rights Reserved Slideshow And Powerpoint Viewer 7 1 Integration By Parts Copyright C Cengage Learning All Rights Reserved




If F X Int X Sinx 1 Cosx Dx And F 0 0 Then The Value Of
The formula for integration by parts is the following ∫ f(x)g′(x) = f(x)g(x)−∫ f′(x)g(x) ∫ f (x) g ′ (x) = f (x) g (x) − ∫ f ′ (x) g (x)The integrand is the product of two function x and sin (x) and we try to use integration by parts in rule 6 as follows Let f(x) = x , g'(x) = sin(x) and therefore g(x) = cos(x) Hence ∫ x sin (x) dx = ∫ f(x) g'(x) dx = ( f(x) g(x) ∫ f'(x) g(x) dx) Substitute f(x), f'(x), g(x) and g'(x) by x , 1, sin(x) and cos(x) respectively to write the integral as = x ( cos(x)) ∫ 1 ( cos(x)) dx Use formula 22 in in the table of integral formulasTheorem 1 Fourier Integral f(x) piecewise continuous righthand / lefthand derivatives exist integral exists Applications of the Fourier Integral Solving differential equations (see 116) & integration, Ex 2) Single pulse, sine integral ∞ −∞ f(x)dx f(x) can be represented by Fourier integral f(x) =1 if x 1




Calc3 1001 By James Bardo Issuu




Ex 7 11 19 Show F X G X Dx 2 F X F X F A X Ex 7 11
Integration Formulas 1 Common Integrals Indefinite Integral Method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = Integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − Integrals of Rational and Irrational Functions 1 1 n x dx Cn x n = ∫ 1 dx x Cln x ∫ = ∫cdx cx C= 2 2 x ∫xdx C= 3 2 3 x ∫x dx C= 2 1 1The value g(x)g(y) is always nonzero for distinct x and y in the interval, for if it was not, the mean value theorem would imply the existence of a p between x and y such that g' (p)=0 The definition of m ( x ) and M ( x ) will result in an extended real number, andF ′ (x) = f (x) for all x in the interval I There is an infinite number of antiderivatives of a function f (x), all differing only by a constant C (F (x) C)′ = F ′(x) C′ = f (x) 0 = f (x) The set of all antiderivatives for a function f (x) is called the indefinite integral of f (x) and is denoted as ∫ f (x)dx = F (x) C, if F
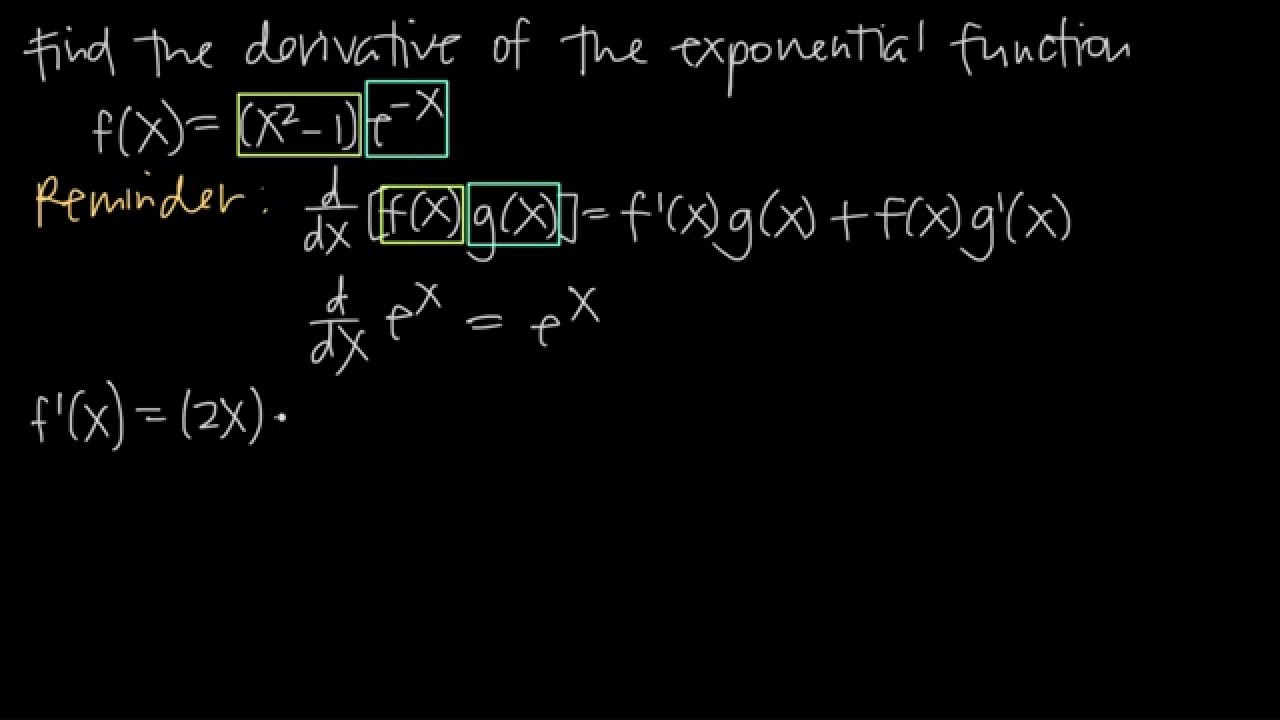



Finding The Derivative Of A Function With E X Kristakingmath Youtube




Integration By Parts Formula F X G X
Here is the formula ∫ f(x)g'(x) dx = f(x)g(x) − ∫ f'(x)g(x) dx You start with the left side of the equation (the antiderivative of the product of two functions) and transform itApr 09, 08 · Re ∫f (x)g (x)dx Thank you So it is Integration by parts, I guess, just expressed with dv as g (x) And u as f (x) By the way, how come when you take the derivative of something, the dx usually isn't written down, but when you go backwards for the integral, you always write down the dx Shouldn't it be used in the answer of the derivativeTo solve I 1, we will use integration by parts Let the first function = f 1 (x) = f (x) and the second function = g 1 (x) = e x Therefore, I 1 = f (x) ∫ e x dx – ∫ df (x)/dx ∫ e x dx dx Or, I 1 = e x f (x) – ∫ e x f ' (x) dx C Substituting the value of I1 in equation (1), we get



Chemical Engineering Chemical Engineering




Engineering Mathematics Notes
Of cousre we can generalize for ∫ 0 a f ( x) f ′ ( a − x) d x Interesting examples would be ∫ 0 π 2 sin nSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreIntegrals cannot distinguish between this and f(x) Because all the functions in question are 2ˇperiodic, we can integrate over any convenient interval of length 2ˇ If f(x) is an odd function, so is f(x)cos(nx), and so a n = 0 for all n 0 If f(x) is an even function, then f(x)sin(nx) is odd, and so b n = 0 for all n 1 Daileda Fourier Coe




Chemical Engineering Chemical Engineering




The Definite Integral And Ftc
Feb 11, 11 · 2) Use the continuity property to deduce there is some neighborhood (c e, c e) ( e>0 ) where g > f in that neighborhood 3) Consider the integral over this interval to find a contradiction To prove 2) stated above use the function g (x)f (x) which is also continuous and you know it has a positive limit at x=cJul 10, · 4 Answers4 Active Oldest Votes 8 Ignoring the constant of integration the answer is (2) ∫f − 1(x)dx = ∫yf ′ (y)dy = yf(y) − ∫f(y)dy (where I have used integration by parts) Hence ∫f − 1(x)dx = f − 1(x)x − g(y) = xf − 1(x) − g(f − 1(x)) ShareMay 30, 18 · From the definition of the definite integral we have, ∫ b a f (x)g(x) dx = lim n→∞ n ∑ i=1(f (x∗ i) g(x∗ i))Δx = lim n→∞( n ∑ i=1f (x∗ i)Δx n ∑ i=1g(x∗ i)Δx) = lim n→∞ n ∑ i=1f (x∗ i)Δx lim n→∞ n ∑ i=1g(x∗ i)Δx =∫ b a f (x) dx∫ b a g(x) dx ∫ a b f ( x) g ( x) d x = lim n → ∞




Integrals Class 12 Formulas Pdf With Notes Vidyakul




Some Properties Of Definite Integrals Proofs Videos And Solved Examples
Power Rule (d/dx) (x n ) = nx n1When finding a definite integral using integration by parts, we should first find the antiderivative (as we do with indefinite integrals), but then we should also evaluate the antiderivative at the boundaries and subtract Using integration by parts Integration by parts intro Integration by parts ∫x⋅cos (x)dx Integration by parts ∫lnMay 19, 18 · Unfortunately there is no such simple rule for integration For example, if f (x) = 1 x and g(x) = ex then we have ∫ f (x) dx = lnx C ∫ g(x) dx = ex C but ∫ f (x)g(x) dx = Ei(x) C where Ei(x) (the exponential integral) is not even an elementary function Answer link




Copyright C Cengage Learning All Rights Reserved Ppt Download




Chapter 4 Maths 3
Integral Calculus Indefinite Integrals Definition A function F(x) is the antiderivative of a function ƒ(x) if for all x in the domain of ƒ, F'(x) = ƒ(x) ƒ(x) dx = F(x) C, where C is a constantBasic Integration Formulas General and Logarithmic IntegralsExample showing the use of the modulus signUse the Substitution Formula, {eq}\displaystyle \int^b_a f(g(x))\cdot g'(x)\;dx = \int^{g(b)}_{g(a)}f(u)\;du {/eq} where g(x) = u, to evaluate the following integral




Fourier Transform To Solve An Integral Frac 1 1 X 2 Cdot E Ix Mathematics Stack Exchange




Integration By Parts Proof Udv Uv Vdu Udv Uv Vdu
F (x)g (x) integral (g (x)*f' (x)) If you can find the second integral you are done Otherwise the problem is more difficult Edit in your example, take f (x) as x and g' (x) as (e^ (02x)) and integration by part works out nicely3 Finding Z f(g(x))g′(x)dx by substituting u = g(x) Example Suppose now we wish to find the integral Z 2x √ 1x2 dx (3) In this example we make the substitution u = 1x2, in order to simplify the squareroot term We shall see that the rest of the integrand, 2xdx, will be taken care of automatically in theThe product rule of integration for two functions say f(x) and g(x) is given by f(x) g(x) = ∫g(x) f'(x) dx ∫f(x) g'(x) dx




Pdf Formula Of Volume Of Revolution With Integration By Parts And Extension



What Is The Integral Of E F X Quora
In this video we learn about function composition Composite functions are combinations of more than one function In this video we learn about f(g(x)) and gF(g(x))g0(x)dx = Z f(u)du = F(u) C where u = g(x) and F0(u) = f(u) Reversing the Product Rule Since we have (f(x)g(x))0 = f(x)g0(x) g(x)f0(x);De nite Integral Version Z b a f(g(x))g0(x)dx= Z g(b) g(a) f(u)du where u= g(x) 11 Example Problems Strategy The idea is to make the integral easier to compute by doing a change of variables 1Start by guessing what the appropriate change of variable u= g(x) should be Usually you choose uto be the function that is \inside" the function 2
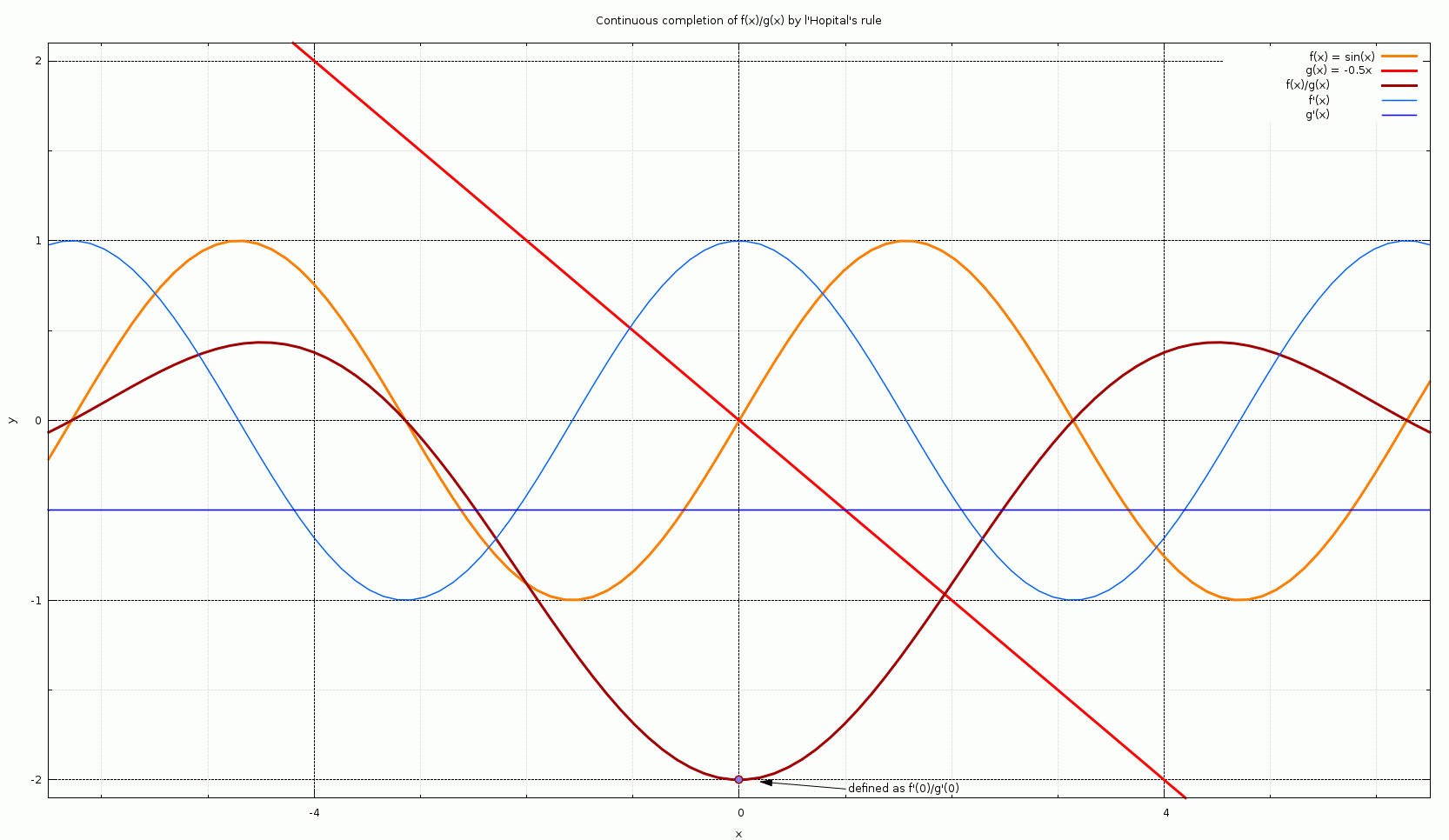



L Hopital S Rule Wikipedia



What Is The Integral Of E F X Quora
F (x)g(x) = f (x)g (x) g(x)f (x) Integrating on both sides of this equation, f (x)g (x) g(x)f (x) dx = f (x)g(x), which may be rearranged to obtain f (x)g (x)dx = f (x)g(x)− g(x)f (x)dx Letting U = f (x) and V = g(x) and observing that dU = f (x)dx and dV = g (x)dx, we obtain the familiar Integration by Parts formula UdV= UV − VdU (1)




Infinite Sequences And Series Formulas For The Remainder Term In Taylor Series Peakd




Axioms For Integration Math Bard Edu Flip Ebook Pages 1 4 Anyflip Anyflip




Functions Defined By Integrals Switched Interval Video Khan Academy




Integration Formulas Trig Definite Integrals Class 12 Pdf




Some Properties Of Definite Integrals Proofs Videos And Solved Examples




Integration By Parts




Pdf A Product Integration Approach Based On New Orthogonal Polynomials For Nonlinear Weakly Singular Integral Equations
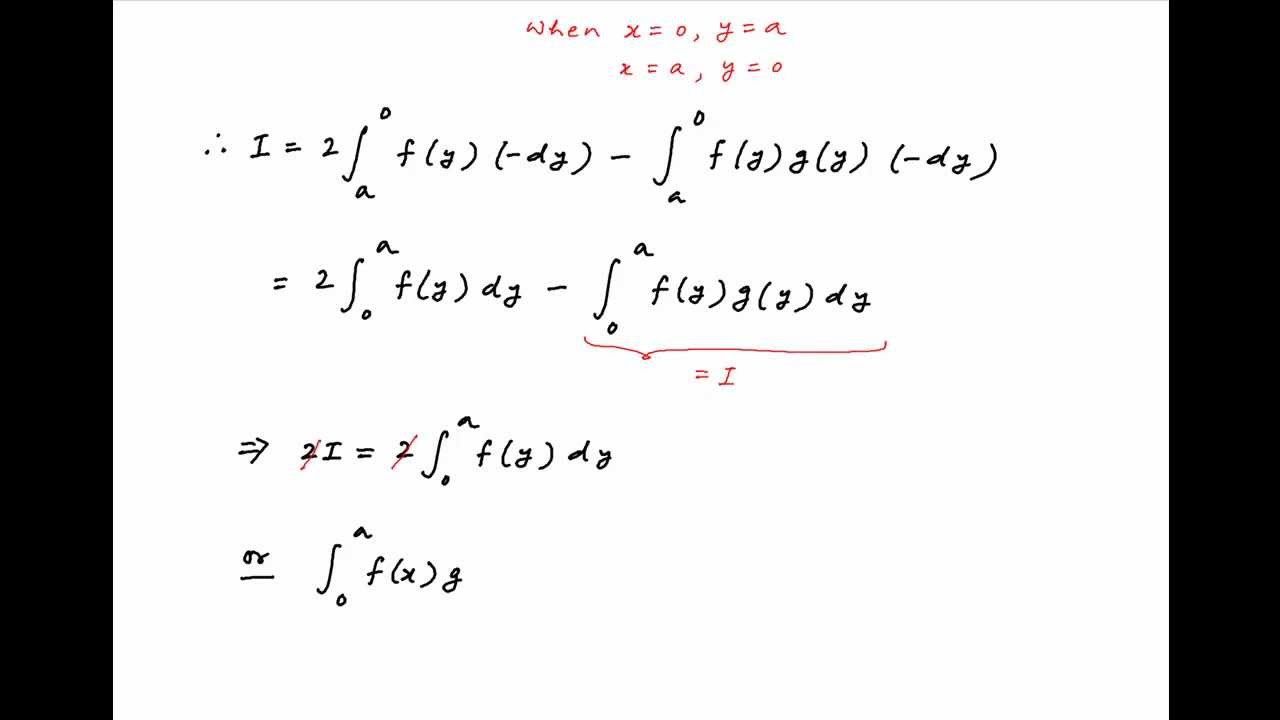



Show That Integral F X G X Between Limits 0 To A Is Equal To Integral F X Between Limits 0 To A Youtube




Integration Of The Form F X F X Dx




Ppt Integrals Powerpoint Presentation Free Download Id




Indefinite Integral Formulas Learning Science




Integration Of E X Sin X Dx Teachoo Maths Integration Class 12



Page407




Unit 4 Integration B C A Study




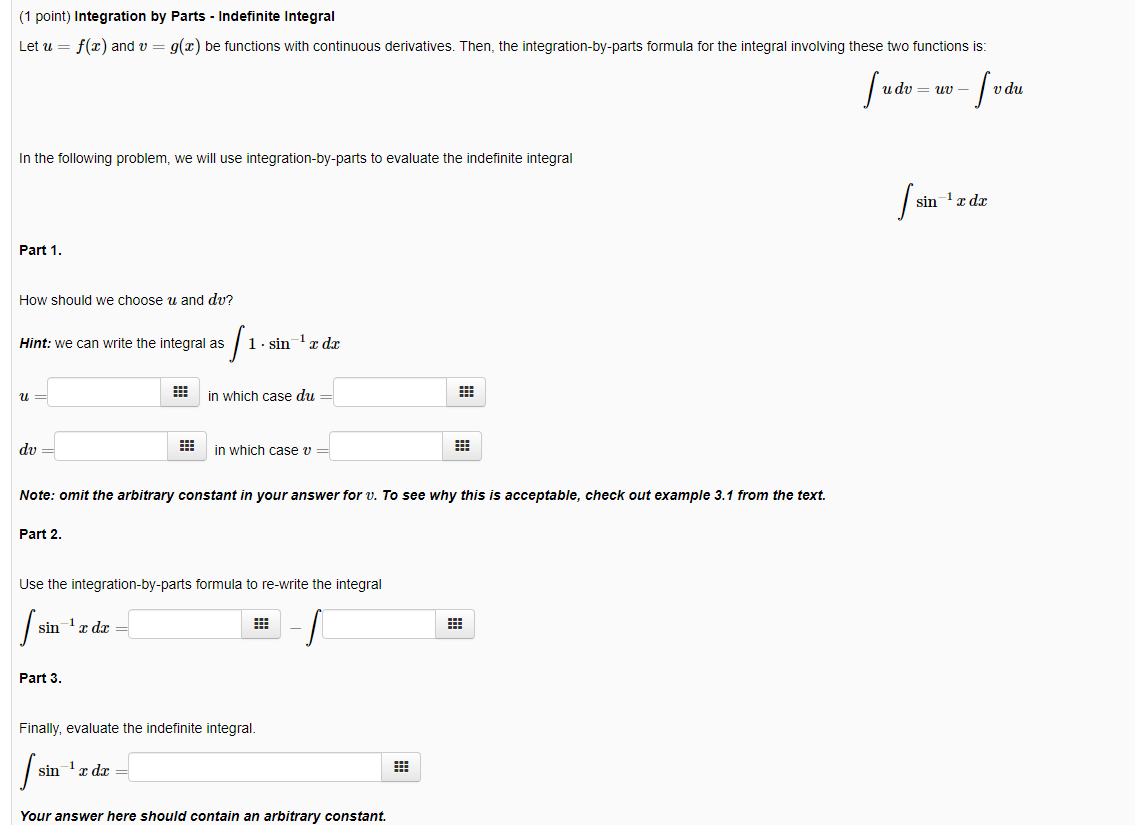
Solved 1 Point Integration By Parts Indefinite Integr Chegg Com




Let F X Int 2 X Dt Sqrt 1 T 4 And G Be The Inverse Of F




Ex 7 9 Direct Integrate X Ex Sin Pi X 4 Dx Ex 7 9




Chapter 6 Integration Ppt Download




How To Do U Substitution Easily Explained With 11 Examples




Finding Derivative With Fundamental Theorem Of Calculus Video Khan Academy




0 1 Integration Ma244 Analysis Iii Solutions Sheet 2




7 Techniques Of Integration Copyright C Cengage Learning All Rights Reserved Slideshow And Powerpoint Viewer 7 1 Integration By Parts Copyright C Cengage Learning All Rights Reserved




Indefinite Integrals Sums Multiples Video Khan Academy



Chapter 11 Techniques Of Integration Pdf Free Download




Solved 5 6 15 G B Use The Substitution Formula F G X Chegg Com




A Quotient Rule Integration By Parts Formula Pages 1 3 Flip Pdf Download Fliphtml5




Integration By Parts Introduction Youtube



Solved 1 Point Integration By Parts Indefinite Integr Chegg Com




Trigonometric




Numerical Differentiation Numerical Integration Notes Math 441 Docsity




1 Functions Limits And Differentiation Pdf Free Download




Mean Value Theorem Wikipedia




Lecture Note 1 Pdf Summation Integral




Misc 43 If F A B X F X Then X F X Dx Is Miscellaneous




All Integration Formulas Complete List Of Integrals Cuemath




How To Integrate Square Root Functions




Packet 21 Integration By Parts Ppt Download




The Definite Integral And Ftc



0 件のコメント:
コメントを投稿